Ecologically-based Granular Synthesis
ICMC 1998, Ann Arbor, Michigan

Damián Keller, Barry Truax
School for the Contemporary Arts
Simon Fraser University

damian_keller@sfu.ca, http://www.sfu.ca/~dkeller
truax@sfu.ca, http://www.sfu.ca/~truax

Introduction

We present a granular synthesis (GS) technique that produces environmental-like sounds using sampled sound grains and meso-time control functions. This approach is related to physical modeling (PM) (Smith, 1992; Välimäki & Takala, 1996) and traditional granular synthesis (GS) (Roads, 1996, 299; Truax, 1988) but we have worked on two issues that have been previously neglected in these techniques. The model (1) produces time patterns at ranges from ten milliseconds to several seconds (meso-level structure), and (2) uses as basic raw material short-duration sampled sound grains with complex spectral dynamics.

Our study focuses on everyday sounds characterized by single processes, such as bouncing, breaking, filling, etc. (Ballas, 1993; Gaver, 1993; Warren & Verbrugge, 1984; Warren et al., 1987). These sounds present dynamic temporal and spectral states that cannot be described solely by deterministic or stochastic models. Stable resonant modes as in some musical instruments (Smith, 1997) or completely stochastic clouds (Roads, 1997) are just two instances of a frequency-time continuum of sound models. Our technique fills some of the gaps along this continuum.

Even though most environmental sounds present wide-ranging variations in their temporal and spectral structure (Handel, 1995, 454), it has been shown that they can easily be identified as belonging to ecologically meaningful classes (Ballas, 1993; McAdams, 1993; Warren et al., 1987). Their global time structure does not lend to synthesis with Fourier-based models and their local spectral complexity is blurred by random sample-based processing (Roads, 1997; Truax, 1994). A new approach for composing at the intersection of the time and frequency domains (Clarke, 1996) is needed.

Granular Synthesis Methods

Granular sounds require high densities of short events to produce aurally convincing sound textures. Therefore, computer music composers have adopted statistically-controlled distributions of grains limited by tendency masks, averages, deviations, probability densities, and other similar methods (Xenakis, 1971; Truax, 1988). Besides the use of quasi-synchronous (periodic) grain streams in formant-wave synthesis (FOF) (Rodet, 1984) and pitch-synchronous granular synthesis (De Poli & Piccialli, 1991), some composers have recently proposed deterministic control methods. Roads (1997) suggests a traditional note-based approach for long grain durations that can be extended to fast grain rates in order to produce micro-temporal and spectral effects. He calls this traditional compositional technique by the name of "pulsar synthesis." Di Scipio (1994) and Truax (1990) have explored the possibilities of controlling granular streams from the output of nonlinear functions. This technique offers good possibilities for the generation of macro-temporal patterns, though up to now only arbitrary mappings of isolated acoustic parameters have been used (e.g., grain frequency, grain duration, etc.). The common trend in all these approaches is to take a time line, isomorphous to absolute time, as the underlying space where the events are placed. In other words, it is in the hands of the composer to make all decisions regarding the duration, density, distribution and organization of the grains.

The ecological approach suggests that time be parsed into informationally relevant events. The perceptual system is constantly searching for patterns of new information. Thus, attention-based processes are triggered by organized transformation, not by redundancy or randomness. To establish ecologically meaningful sound events, the grain distributions and the spectral changes have to be controlled from parameters defined by a higher level transformation. This transformation needs to be constrained to a finite event which is feasible, at least in theory, within our day-to-day environment. In other words, we are not working on an abstract time line, but from a representation which parses time into ecologically-constrained events.

Looking at the granular approach as a two-stage method, we can differentiate the control-function generation from the sound synthesis stage. First, we establish a time-frequency grid of grains by means of analysis (Short-Time Fourier Transform, Wavelet Transform) or algorithmic generation (screen, cloud, density). Then, we produce the sound by placing either synthesized grains (e.g., sine waves, filter parameters) or sampled-sound grains (from one or several sound files).

Fig 1. Granular synthesis as a two-stage method.
The control functions establish a time-frequency grid
where the grains taken from a sound database are placed.

Control Functions

Whether the control functions are derived from analysis, or generated algorithmically, similarly to signals, they can be classified in two broad classes: (1) deterministic, and (2) stochastic. Deterministic processes can be produced by linear or nonlinear dynamical systems. Among the properties of linear systems we find: (a) the output is independent of previous inputs; (b) their impulse response is finite (FIR); (c) they are stable. Examples of linear systems are the filters used in subtractive synthesis. By introducing feedback, the output of the system is made dependent on previous inputs. Thus, for some parameters the system may present instability and nonlinearity.

Based on these general classes of control functions, it is possible to group the synthesis methods in GS (as opposed to the analysis methods) in two rather simplified categories: (1) synchronous, mostly based on deterministic functions; and (2) asynchronous, based on stochastic functions.

Synchronous methods are found in FOF synthesis, VOSIM, quasi-synchronous GS, and pitch-synchronous GS. Asynchronous methods have been used in synthesis by ‘screens’ (Xenakis, 1971), real-time GS (Truax, 1988), FOG synthesis, and pulsar synthesis. There are two control variables: (1) the delay between grains for a single stream, and (2) the synchronicity among grains in different streams. In ecologically-based GS, we use the term phase-synchronous for several streams that share the same grain rate, and phase-asynchronous for independent streams.

Fig 2. Classification of granular synthesis methods based on the characteristics of their grain generators.

Sound Database

As mentioned previously, control functions define local parameters in granular synthesis. The relevance of each of these parameters depends on which GS approach is adopted. For example, envelope shape is important in FOF synthesis because this local parameter determines the bandwidth of the resulting formant. By contrast, the same parameter in asynchronous GS has an effect dependent on the sound file used (Keller, 1998). Random sample-based processing causes spectral "blurring" and the sound is further modified by the complex interaction of overlapping spectrally rich grains. In part, this explains the gap between GS techniques that use simple synthetic grains to try to synthesize existing sounds, and the granular compositional approaches that start from more interesting and complex grains which produce less predictable results. "Tell me what grain waveform you choose and I'll tell you who you are."

GS techniques have used three types of local waveforms: (1) sine waves, in FOF synthesis; (2) FIR filters derived by spectral analysis, in pitch-synchronous synthesis; and (3) arbitrary sampled sounds, in asynchronous, FOG, and pulsar synthesis. Given that the local spectrum affects the global sound structure, we use waveforms that can be parsed in short durations (20 to 200 ms) without altering the complex characteristics of the original sampled sound. Thus, we use water drops for stream-like sounds, or pieces of bottles crashing for breaking-glass sounds.

Methods

The synthesis technique used in our study is implemented in Csound (Vercoe, 1993), and the grain events are generated with our own score generator and CMask (Bartetzki, 1997). The local parameters provided by the score determine the temporal structure of the resulting sounds. These parameters are processed by one or several instruments in the orchestra. The instruments function as grain stream generators. There are three possible configurations: (1) a single stream generator, for bouncing sounds and rugged textures; (2) parallel phase-asynchronous stream generators, for water stream-like sounds; (3) parallel phase-synchronous stream generators, for dense wind-like sounds.

The procedure for modeling environmental-like sounds consists of four stages:
1. Collect several samples of everyday sounds produced by objects excited by physical agencies, such as running water or fire, and objects excited by biological agencies, e.g., cracking wood, struck metal.
2. Analyze the temporal patterns and the spectral characteristics of the samples.
3. Extract grains to be used in the Csound synthesis language and define the meso-scale temporal behavior of the simulation.
4. Synthesize the sounds and compare the results with the original samples.

Bounce

The bounce pattern can be approximated by an exponential curve or by a recursive equation. The former can only be used for one instance of the class of bounce sounds. On the other hand, the latter provides a general representation of all possible forms of bounce patterns. It can easily be adjusted just by changing the damping parameter. Thus, we get a family of exponential curves with different rates of damping or grain rate acceleration.

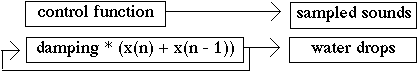
Fig 3. Simple bounce model.

Water stream

By using several samples of drop sounds, the spectral changes over time can be approximated. When the grain duration is increased, several grains overlap. This causes a formant region which is perceptually interpreted as a water stream sound. This model provides a smooth transition between discrete drops and fused, dense water sounds (Keller, 1998).

Texture scraping

In the scraping simulation the control function is periodic but the sound is random. Friction between two rough surfaces should produce a noisy spectrum, but this spectrum should vary depending on the speed of scraping and the roughness of the surfaces. This is, of course, a loose metaphor. Nevertheless, the results are better than using the approach reported by Gaver (1993, 233), i.e., frequency of band-limited noise corresponding to dragging speed, and bandwidth correlated to roughness of the surface.

Summary

In ecologically-based GS, the total spectral result is produced by the interaction of the local waveforms with the meso-scale time patterns. Thus, the output is characterized by emergent properties, which are not present in either global or local parameters. For example, by using a single bottle-bounce grain with exponential acceleration, we have reproduced the rising pitch that can be heard in real-world bouncing bottles. Comparable phenomena have been observed in simulated water-drop sounds and rugged-texture sounds.

As pointed out by Dannenberg (1996), there is a lack of research in sound organization in time scales ranging from ten milliseconds to several seconds. Most sound synthesis efforts have concentrated on micro-scale, overlooking the perceptual relevance of longer time scale organization (Keller & Silva, 1995). Our research confirms that these higher-level patterns strongly influence our perception of ecologically meaningful sounds (Bregman, 1990, 484).

The Csound and Cmask code and the samples used to produce the examples can be found at Download Stop. Excerpts taken from the piece ". . . soretes de punta." (Keller, 1998) will be available at the earsay site.

Sound Examples

The sound examples can be heard at http://www.sfu.ca/sonic-studio/EcoModelsComposition/SoundExamples.html.

Acknowledgements

The School for the Contemporary Arts, Simon Fraser University, has provided financial support for this project. This work forms part of the first author's MFA thesis research project.

References

Ballas, J.A. (1993). Common factors in the identification of an assortment of brief everyday sounds. Journal of Experimental Psychology: Human Perception and Performance, 19(2), 250-267.

Bartetzki, A. (1997). CMask. Software package. Berlin: STEAM.

Bregman, A.S. (1990). Auditory Scene Analysis: The Perceptual Organization of Sound. Cambridge, MA: MIT Press.

Cavaliere, S., & Piccialli, A. (1997). Granular synthesis of musical signals, Musical Signal Processing, C. Roads, S.T. Pope, A. Piccialli, & G. De Poli (Eds.). Lisse: Swets & Zeitlinger, 155-186.

Clarke, J.M. (1996). Composing at the intersection of time and frequency. Organised Sound, 1(2), 107-117.

Dannenberg, R.B. (1996). A perspective on computer music. Computer Music Journal, 20(1), 52-56.

De Poli, G., & Piccialli, A. (1991). Pitch-synchronous granular synthesis, Representations of Musical Signals, G. De Poli, A. Piccialli, & C. Roads (Eds.). Cambridge, MA: MIT Press.

Florens, J.-L., & Cadoz, C. (1991). The physical model: modeling and simulating the instrumental universe, Representations of Musical Signals, G. De Poli, A. Piccialli, & C. Roads (Eds.). Cambridge, MA: MIT Press, 227-268.

Gaver, W.W. (1993). Synthesizing auditory icons. Proceedings of the INTERCHI 1993. New York, NY: ACM, 24-29.

Handel, S. (1995). Timbre perception and auditory object identification, Hearing, B.C.J. Moore (Ed.). New York, NY: Academic Press.

Keller, D. (1998). ". . . soretes de punta." Harangue 2. Burnaby, BC: earsay productions.

Keller, D., & Silva, C. (1995). Theoretical outline of a hybrid musical system. Proceedings of the II Brazilian Symposium on Computer Music. Canela, RS: Eduardo Reck Miranda.

McAdams, S. (1993). Recognition of sound sources and events, Thinking in Sound, S. McAdams and E. Bigand (Eds.). Oxford: Oxford University Press.

Roads, C. (1996). The Computer Music Tutorial. Cambridge, MA: MIT Press.

Roads, C. (1997). Sound transformation by convolution, Musical Signal Processing, C. Roads, S.T. Pope, A. Piccialli, & G. De Poli (Eds.). Lisse: Swets & Zeitlinger, 411-438.

Rodet, X. (1984). Time-domain formant wave-function synthesis. Computer Music Journal, 8(3), 9-14.

Smith, J.O. (1992). Physical modeling using digital waveguides. Computer Music Journal, 16(4), 74-87.

Smith, J.O. (1997). Acoustic modeling using digital waveguides, Musical Signal Processing, C. Roads, S.T. Pope, A. Piccialli, & G. De Poli (Eds.). Lisse: Swets & Zeitlinger, 221-263.

Truax, B. (1988). Real-time granular synthesis with a digital signal processor. Computer Music Journal, 12(2), 14-26.

Truax, B. (1990). Chaotic non-linear systems and digital synthesis: an exploratory study. Proceedings of the International Computer Conference. San Francisco: ICMA, 100-103.

Truax, B. (1994). Discovering inner complexity: time shifting and transposition with a real-time granulation technique. Computer Music Journal, 18(2), 38-48.

Valimaki, V., & Takala, T. (1996). Virtual musical instruments - natural sound using physical models, Organised Sound, 1(2), 75-86.

Vercoe, B. (1993). Csound. Software package. Cambridge, MA: MIT Media Lab.

Warren, W.H., & Verbrugge, R.R. (1984). Auditory perception of breaking and bouncing events: a case study in ecological acoustics. Journal of Experimental Psychology: Human Perception and Performance, 10, 704-712.

Warren, W.H., Kim, E.E., & Husney, R. (1987). The way the ball bounces: visual and auditory perception of elasticity and control of the bounce pass. Perception, 16, 309-336.

Xenakis, I. (1971). Formalized Music. Bloomington, IN: Indiana University Press.

Référence: http://www.sfu.ca/~dkeller/EcoGranSynth/EGSpaper.html